Почему (a | b) эквивалентно a - (a & b) + b?

Question

Я искал способ сделать BITOR() с базой данных Oracle и наткнулся на предложение просто использовать BITAND() вместо этого, заменив BITOR (a, b) на + b - BITAND (a, b).

Я проверил его вручную несколько раз и подтвердил, что он работает для всех двоичных чисел, о которых я мог думать, но я не могу придумать быстрое математическое доказательство того, почему это правильно.
Может ли кто-нибудь просветить меня?

Answer 1

A & B - это набор бит, которые включены как в A, так и в B. A - (A & B) оставляет вас со всеми этими битами, которые находятся только в A. Добавьте B к этому, и вы получите все биты, которые включены в A или те, которые включены в B.

Простое добавление A и B не будет работать из-за переноса, где оба имеют бит 1 бит. Сначала удаляя биты, общие для A и B, мы знаем, что (A- (A & B)) не будет иметь никаких бит вместе с B, поэтому их объединение гарантировано не приведет к переносу.

Answer 2

Представьте, что у вас есть два двоичных числа: a и b. И предположим, что эти числа никогда не имеют 1 в одном и том же бите одновременно, то есть если a имеет 1 в некотором бите, b всегда имеет 0 в соответствующем бите. И в другом направлении, если b имеет 1 в некотором разряде, тогда a всегда имеет 0 в этом бите. Например

a = 00100011 
b = 11000100 

Это было бы примером a и b, удовлетворяющих этому условию. В этом случае легко видеть, что a | b будет точно таким же, как a + b.

a | b = 11100111 
a + b = 11100111 

Давайте теперь возьмем два числа, которые нарушают наши условия, то есть два числа, по крайней мере, один 1 в некоторых общих бит

a = 00100111 
b = 11000100 

Является a | b же, как a + b в этом случае? No

a | b = 11100111 
a + b = 11101011 

Почему они разные? Они отличаются друг от друга, потому что когда мы имеем + бит, который имеет 1 в обоих числах, мы производим так называемый перенос: результирующий бит равен 0, а 1 переносится на следующий бит влево: 1 + 1 = 10. Операция | не кэрри, так 1 | 1 снова только 1.

Это означает, что разница между a | b и a + b происходит тогда и только тогда, когда числа имеют по крайней мере один 1 в общем немного. Когда мы суммируем два числа с 1 общим битом, эти общие биты добавляются «дважды» и производят перенос, который разрушает сходство между a | b и a + b.

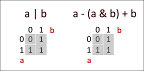
Теперь взгляните на a & b. Что вычисляет a & b? a & b дает номер, который имеет 1 во всех битах, где оба a и b имеют 1.В нашем последнем примере

a =  00100111 
b =  11000100 
a & b = 00000100 

Как вы видели выше, это именно те биты, которые делают a + b отличаются от a | b. 1 в a & b указывают все позиции, в которых будет происходить перенос.

Теперь, когда мы делаем a - (a & b) мы эффективно удалить (вычитать) все «нарушители» биты из a и только такие биты

a - (a & b) = 00100011 

Числа a - (a & b) и b не имеют общих 1 бит, что означает, что если мы добавим a - (a & b) и b мы не будем работать в ручной клади, и, если вы думаете об этом, мы должны в конечном итоге с тем же результатом, как если бы мы просто сделали a | b

a - (a & b) + b = 11100111 

Answer 3

A & B = C, где любые оставшиеся бит в C заданы как в A, так и в B.
Либо AC = D, либо BC = E устанавливает только эти общие бит в 0. Несущий эффект отсутствует, поскольку 1 -1 = 0.
D + В или Е + А подобен А + В, за исключением того, потому что мы вычитали & В ранее не будет никакого переноса из-за очистив все обычно установленные биты в D или E.

Конечным результатом является что AA & B + B или BA & B + A эквивалентно A | B.

Вот таблица истинности, если она по-прежнему сбивает с толку:

 
A | B | OR A | B | & A | B | - A | B | + 
---+---+---- ---+---+--- ---+---+--- ---+---+--- 
0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 
0 | 1 | 1 0 | 1 | 0 0 | 1 | 0-1 0 | 1 | 1 
1 | 0 | 1 1 | 0 | 0 1 | 0 | 1 1 | 0 | 1 
1 | 1 | 1 1 | 1 | 1 1 | 1 | 0 1 | 1 | 1+1

Обратите внимание перенесенных строки в + и - операции, мы избегаем тех, потому что A- (A & B) устанавливает случаи были оба бита в A и B от 1 до 0 в A, а затем добавление их обратно из B также приводит к другим случаям, если в A или B было 1, но не там, где оба имели 0, поэтому таблица истинности OR и A- (A & B) + B таблица истинности идентичны.

Другой способ глазного яблока - видеть, что A + B почти похож на A | B, за исключением переноса в нижнем ряду. A & B изолирует этот нижний ряд для нас, A-A & B перемещает те изолированные изолированные в два ряда в таблице +, а (A-A & B) + B становится эквивалентным A | B.

В то время как вы могли бы коммутировать это A + B- (A & B), я боялся возможного переполнения, но это было неоправданным, кажется:

#include <stdio.h> 
int main(){ unsigned int a=0xC0000000, b=0xA0000000; 
printf("%x %x %x %x\n",a, b,  a|b,  a&b); 
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); } 

c0000000 a0000000 e0000000 80000000 
60000000 40000000 e0000000 e0000000 

Редактировать: Так что я написал это раньше были ответы, затем на моем домашнем соединении было около 2 часов простоя, и мне, наконец, удалось опубликовать его, заметив только после этого, что он был должным образом ответил дважды. Лично я предпочитаю ссылаться на таблицу истинности, чтобы выработать побитовые операции, поэтому я оставлю ее на случай, если она кому-то поможет.

Answer 4